Greek Digits

The use of Greek digits, also known as Greek numerals, is a fascinating aspect of ancient Greek mathematics and culture. In contrast to the modern Hindu-Arabic numeral system used globally today, the Greek system employed letters of the Greek alphabet to represent numbers. This unique approach not only reflects the ingenuity and simplicity of ancient Greek mathematics but also underscores the complexities and limitations of their numerical representations.
Introduction to Greek Digits

Greek digits were based on the 24 letters of the Greek alphabet, with the first nine letters (alpha to theta) representing the numbers 1 to 9, the next nine letters (iota to koppa) representing the tens (10 to 90), and the last set of letters representing the hundreds (100 to 900). This system, while innovative for its time, posed challenges for mathematical operations and representations beyond certain values.
Evolution of the Greek Numeral System
The evolution of the Greek numeral system is closely tied to the development of Greek mathematics and astronomy. Early Greek mathematicians, such as Pythagoras and Euclid, contributed significantly to the field, laying the foundations for later mathematicians like Archimedes, who is renowned for his contributions to geometry and the method of exhaustion, a precursor to integration. The use of Greek digits facilitated these developments, albeit with limitations that would eventually be addressed by the adoption of the Hindu-Arabic numeral system in Europe during the Middle Ages.
| Greek Letter | Corresponding Number |
|---|---|
| Alpha (α) | 1 |
| Beta (β) | 2 |
| Gamma (γ) | 3 |
| ... to Theta (θ) | ... to 9 |
| Iota (ι) | 10 |
| Kappa (κ) | 20 |
| Lambda (λ) | 30 |
| ... to Koppa (Ϙ) | ... to 90 |
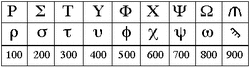
| Rho (ρ) | 100 |
| ... to Omega (ω) modified | ... to 900 |
Technical Specifications and Challenges

From a technical standpoint, the Greek numeral system posed significant challenges, particularly for representing large numbers and performing complex mathematical operations. The lack of a zero concept and the cumbersome nature of representing numbers above 999 (which required additional notation) limited the system’s utility for advanced calculations and astronomical observations. Despite these limitations, Greek mathematicians made groundbreaking discoveries, showcasing their ingenuity and the potential of mathematical reasoning.
Practical Applications and Historical Context
The practical applications of Greek digits extended beyond pure mathematics into engineering, architecture, and commerce. The construction of iconic structures like the Parthenon and the sophisticated water supply systems of ancient Greek cities attest to the application of mathematical principles in everyday life. However, the system’s constraints became apparent as Greek mathematics and astronomy evolved, necessitating more efficient and expressive numeral systems.
Key Points
- The Greek numeral system utilized the Greek alphabet to represent numbers, reflecting both ingenuity and limitations in numerical representation.
- The system was based on the 24 letters of the Greek alphabet, divided into groups representing ones, tens, and hundreds.
- Greek mathematicians, despite the system's constraints, made significant contributions to mathematics and astronomy, laying the groundwork for future scientific advancements.
- The limitations of the Greek numeral system, including the lack of a zero concept and difficulties in representing large numbers, eventually led to the adoption of the Hindu-Arabic numeral system in Europe.
- The use of Greek digits in practical applications, such as engineering and commerce, underscores the adaptability and resourcefulness of ancient Greek civilization.
Conclusion and Forward-Looking Implications
In conclusion, the study of Greek digits offers a fascinating glimpse into the development of mathematical thought and the challenges faced by ancient civilizations in representing numbers. The evolution of numeral systems, from the Greek digits to the modern Hindu-Arabic system, highlights the importance of flexibility and expressiveness in mathematical notation for advancing scientific knowledge. As we continue to push the boundaries of mathematical understanding and its applications, the historical context and technological limitations of ancient numeral systems serve as a reminder of the ingenuity and perseverance of mathematicians and scientists across centuries.
What was the primary limitation of the Greek numeral system?
+The primary limitation of the Greek numeral system was its inability to efficiently represent large numbers and perform complex mathematical operations due to the lack of a zero concept and the cumbersome nature of its notation.
How did Greek mathematicians contribute to the field despite the limitations of their numeral system?
+Greek mathematicians made significant contributions by focusing on geometric and astronomical studies, where the limitations of their numeral system were less hindering. They developed sophisticated methods for calculating areas, volumes, and astronomical distances, laying foundational principles for later scientific advancements.
What is the significance of studying ancient numeral systems like the Greek digits?
+Studying ancient numeral systems provides insights into the historical development of mathematics, underscores the challenges and ingenuity of ancient civilizations, and highlights the importance of adaptable and expressive mathematical notation for scientific progress.



